Goodness-of-fit assessment of the fitted model.

gof() calculates omnibus discrepancy measures and their Bayesian \(p\)-values for the fitted model using the posterior predictive check approach.

Usage

gof(fit, stats = c("Freeman_Tukey", "deviance"), cores = 1L, plot = TRUE, ...)

Arguments

fit: An occumbFit object.
stats: The discrepancy statistics to be applied.
cores: The number of cores to use for parallelization.
plot: Logical, determine if draw scatter plots of the fit statistics.
...: Additional arguments passed to the default plot method.

Value

A list with the following named elements:

stats: The discrepancy statistics applied.
p_value: Bayesian \(p\)-value.
stats_obs: Discrepancy statistics for observed data.
stats_rep: Discrepancy statistics for repeated data.

Details

A discrepancy statistic for the fitted model is obtained using a posterior predictive checking procedure. The following statistics are currently available:

Freeman-Tukey statistics (default): \(T_{\textrm{FT}} = \sum_{i,j,k}\left(\sqrt{y_{ijk}} - \sqrt{E(y_{ijk} \mid \pi_{ijk})}\right)^2\)
Deviance statistics: \(T_{\textrm{deviance}} = -2 \sum_{j,k} \log \textrm{Multinomial}(\boldsymbol{y}_{jk} \mid \boldsymbol{\pi}_{jk})\)

where \(i\), \(j\), and \(k\) are the subscripts of species, site, and replicate, respectively, \(y_{ijk}\) is sequence read count data, \(\pi_{ijk}\) is multinomial cell probabilities of sequence read counts, \(E(y_{ijk} \mid \pi_{ijk})\) is expected value of the sequence read counts conditional on their cell probabilities, and \(\log \textrm{Multinomial}(\boldsymbol{y}_{jk} \mid \boldsymbol{\pi}_{jk})\) is the multinomial log-likelihood of the sequence read counts in replicate \(k\) of site \(j\) conditional on their cell probabilities.

The Bayesian \(p\)-value is estimated as the probability that the value of the discrepancy statistics of the replicated dataset is more extreme than that of the observed dataset. An extreme Bayesian \(p\)-value may indicate inadequate model fit. See Gelman et al. (2014), Kéry and Royle (2016), and Conn et al. (2018) for further details on the procedures used for posterior predictive checking.

Computations can be run in parallel on multiple CPU cores where the cores argument controls the degree of parallelization.

References

P. B. Conn, D. S. Johnson, P. J. Williams, S. R. Melin and M. B. Hooten. (2018) A guide to Bayesian model checking for ecologists. Ecological Monographs 88:526--542. doi:10.1002/ecm.1314

A. Gelman, J. B. Carlin, H. S. Stern D. B. Dunson, A. Vehtari and D. B. Rubin (2013) Bayesian Data Analysis. 3rd edition. Chapman and Hall/CRC. http://www.stat.columbia.edu/~gelman/book/

M. Kéry and J. A. Royle (2016) Applied Hierarchical Modeling in Ecology --- Analysis of Distribution, Abundance and Species Richness in R and BUGS. Volume 1: Prelude and Static Models. Academic Press. https://www.mbr-pwrc.usgs.gov/pubanalysis/keryroylebook/

Examples

# \donttest{
# Generate the smallest random dataset (2 species * 2 sites * 2 reps)
I <- 2 # Number of species
J <- 2 # Number of sites
K <- 2 # Number of replicates
data <- occumbData(
    y = array(sample.int(I * J * K), dim = c(I, J, K)),
    spec_cov = list(cov1 = rnorm(I)),
    site_cov = list(cov2 = rnorm(J),
                    cov3 = factor(1:J)),
    repl_cov = list(cov4 = matrix(rnorm(J * K), J, K)))

# Fitting a null model
fit <- occumb(data = data)
#> 
#> Processing function input....... 
#> 
#> Done. 
#>  
#> Compiling model graph
#>    Resolving undeclared variables
#>    Allocating nodes
#> Graph information:
#>    Observed stochastic nodes: 4
#>    Unobserved stochastic nodes: 31
#>    Total graph size: 133
#> 
#> Initializing model
#> 
#> Adaptive phase..... 
#> Adaptive phase complete 
#>  
#> 
#>  Burn-in phase, 10000 iterations x 4 chains 
#>  
#> 
#> Sampling from joint posterior, 10000 iterations x 4 chains 
#>  
#> 
#> Calculating statistics....... 
#> 
#> Done. 

# Goodness-of-fit assessment
gof_result <- gof(fit)

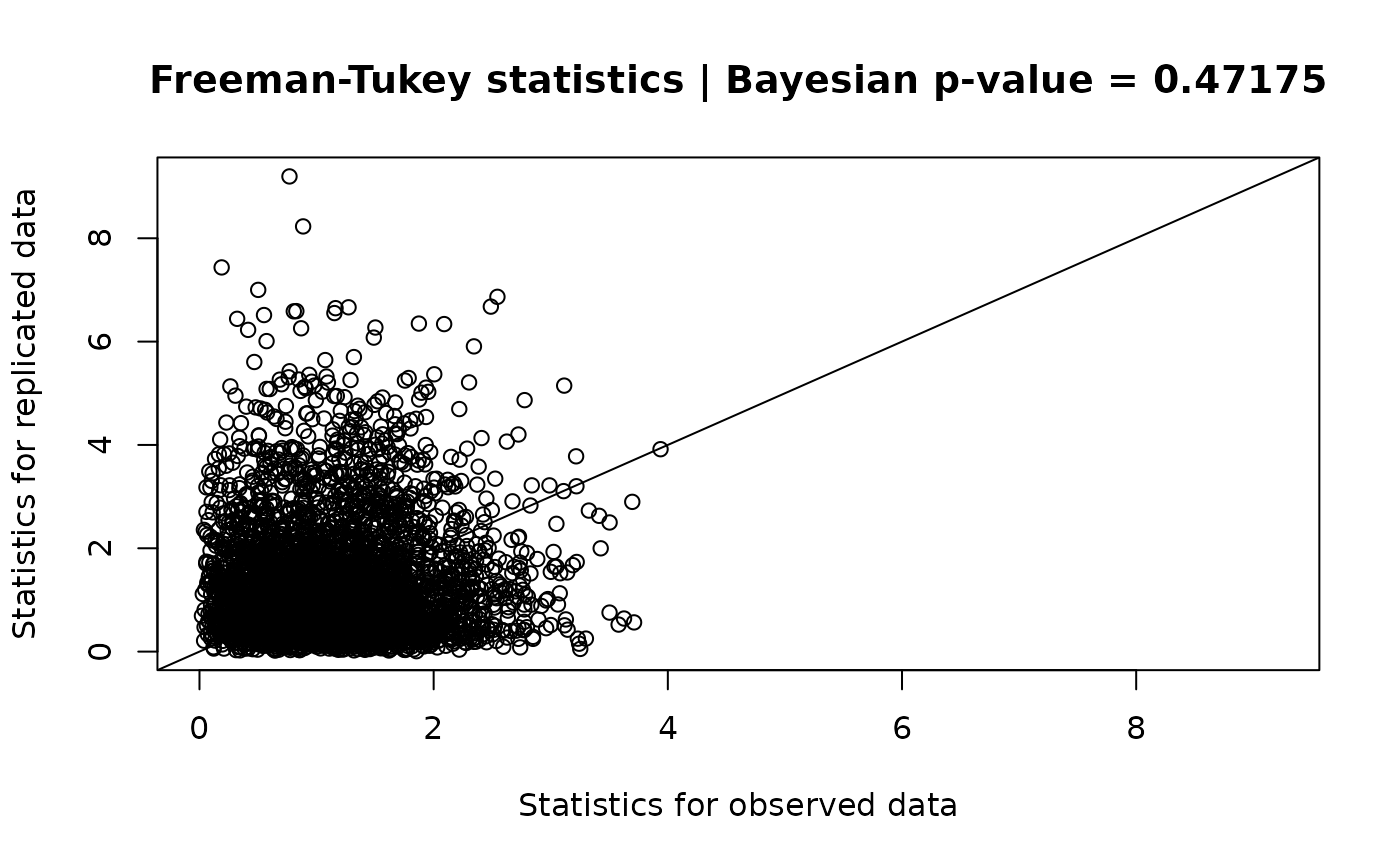gof_result
#> Posterior predictive check for an occumbFit object:
#>  Statistics: Freeman-Tukey 
#>  p-value:    0.47175 
#>  Discrepancy statistics for observed data:   1.18 (mean), 0.61 (sd) 
#>  Discrepancy statistics for replicated data: 1.32 (mean), 1.1 (sd) 
# }